Some of the torquiest problems ever!
Simple torque problems
|
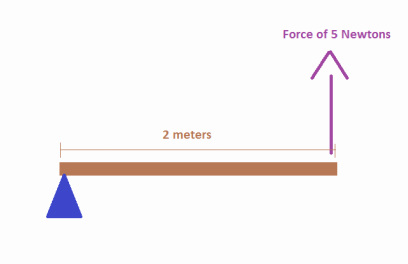
Example 1
A force of 5.0 N is applied at the end of a lever that has a length of 2.0 meters. If the force is applied directly perpendicular to the the lever, as shown in the diagram, what is the magnitude of the torque acting the lever? Torque = Force * lever Since we know both the amount of force and the length of the lever, figuring torque out become very easy for us. Torque = 5.0 N * 2.0 m Torque = 10 N*m |
|
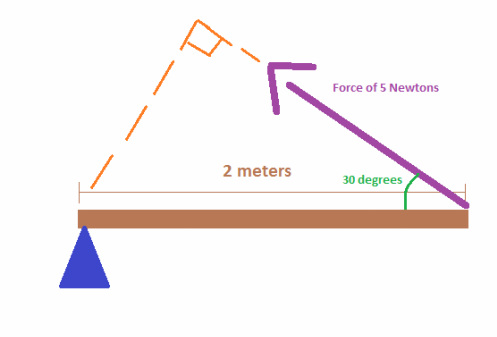
Example 2
If the same force as in example 1 is applied at an angle of 30 degrees at the end of the 2.0 meter lever, what will be the magnitude of the torque? Torque = Force * lever Torque = F * rsin(theta) We know the force, the radius, and the angle, so to find torque we simply have to plug the numbers into the equation. T = (5 N)(2 m)sin(30) T = 10sin(30) T = 5 Nm |
see saw PRoblem
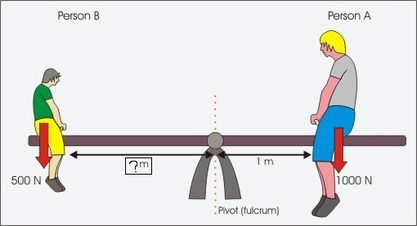
What is a see-saw problem?
A see-saw problem is a problem in which there is a see-saw, a pivot (fulcrum), and a torque. In a see-saw problem in order for the see-saw to be in balance:
(distance1 * mass1) = (distance2 * mass2)
For example, say there are 2 people: Person A and Person B. Person B weighs 500 N while Person A weighs 1000 N. The distance of person A from the center is 1 meter. How far is Person B from the center?
In order to find the answer, we must set the problem into the equation
(D1 * M1) = (D2 * M2)
(500 N * M1) = (1000 N * 1 m)
(500 N)(? m) = 1000 Nm
m = 2 meter
Person B is 2 meters away from the center of the see-saw.
A see-saw problem is a problem in which there is a see-saw, a pivot (fulcrum), and a torque. In a see-saw problem in order for the see-saw to be in balance:
(distance1 * mass1) = (distance2 * mass2)
For example, say there are 2 people: Person A and Person B. Person B weighs 500 N while Person A weighs 1000 N. The distance of person A from the center is 1 meter. How far is Person B from the center?
In order to find the answer, we must set the problem into the equation
(D1 * M1) = (D2 * M2)
(500 N * M1) = (1000 N * 1 m)
(500 N)(? m) = 1000 Nm
m = 2 meter
Person B is 2 meters away from the center of the see-saw.
LAdder Problem
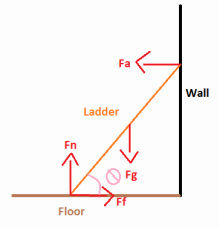
What is a ladder problem?
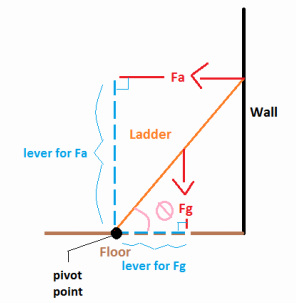
A ladder problem is a problem dealing with a ladder. They are special because the problem is simple, but the calculation becomes complicated. In a ladder problem there are usually 4 forces:
Fa = the force exerted on the ladder by the wall
Ff = the force of friction between the ladder and the ground
Fn = Normal Force, exerted by the ground on the ladder
Fg = the weight of the ladder which is exerted downward
Since the ladder is in static equilibrium the net horizontal force (Fa + Ff) = 0
The same is true for the vertical forces. Fn + Fg = 0
If we pick the bottom of the ladder as our piviot point then Fn and Ff both will not generate torques. Since that eliminates two forces and possible torques right away, this is generally done in ladder problems.
A ladder problem is a problem dealing with a ladder. They are special because the problem is simple, but the calculation becomes complicated. In a ladder problem there are usually 4 forces:
Fa = the force exerted on the ladder by the wall
Ff = the force of friction between the ladder and the ground
Fn = Normal Force, exerted by the ground on the ladder
Fg = the weight of the ladder which is exerted downward
Since the ladder is in static equilibrium the net horizontal force (Fa + Ff) = 0
The same is true for the vertical forces. Fn + Fg = 0
If we pick the bottom of the ladder as our piviot point then Fn and Ff both will not generate torques. Since that eliminates two forces and possible torques right away, this is generally done in ladder problems.
|
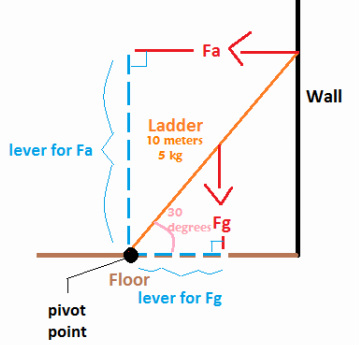
Since there are 2 forces, there will be 2 different torques.
Now examine each of the torques. Fg will create a clockwise torque and Fa will produce a counterclockwise torque. ______________________________________________ Now the example: The ladder is 10 meters long. The force Fg pulls down from the center of the ladder. If the 5 kg ladder is 30 degrees above the horizontal ground, what is the clockwise torque, counter-clockwise torque, Fg, and Fa? Lets find the torque of Fg first: T = Fg * rsin(theta) So what is Fg? Fg = ma Fg = (5 kg)(10) Fg = 50 N T = 50 * 5sin(30) --> Fg radius is half of Fa radius. T = 50 * 2.5 T = 125 Nm Since the latter is at rest, both torques should be equal. This means that if torque of Fg is 125 Nm, the torque of Fa must also be 125 Nm. Now lets start with finding the torque of Fa: T = Fa * lever T = F * rsin(theta) 125 = F * 10sin(90-30) --> the angle is not 30 125 = F * 8.66 125 = 8.66F Fa= 14.43 N |